Right triangle

Rtriangle

Illustration to Euclid's proof of the Pythagorean theorem2

Teorema

thm mediane

Right triangle or right-angled triangle is a triangle in which one of the angles is a right angle (that is, a 90-degree angle). The relation between the sides and angles of a right triangle is the basis for trigonometry.

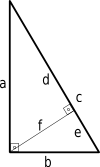
The side opposite the right angle is called the hypotenuse (side c in the figure below). The sides adjacent to the right angle are called the legs (sides a and b in the figure below).

Properties and formulas

A right triangle has several important properties and formulas:

• The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the legs (a and b): a² + b² = c².
• The trigonometric functions (sine, cosine, and tangent) can be defined in the context of a right triangle. For an angle θ:
  • The sine of θ is the ratio of the length of the opposite leg to the length of the hypotenuse.
  • The cosine of θ is the ratio of the length of the adjacent leg to the length of the hypotenuse.
  • The tangent of θ is the ratio of the length of the opposite leg to the length of the adjacent leg.
• The area of a right triangle can be found using the formula: 1/2 * base * height, where the base and height are the lengths of the two legs.

Special right triangles

There are two special types of right triangles:

• A 45°-45°-90° triangle, where the legs are of equal length and the hypotenuse is √2 times the length of a leg.
• A 30°-60°-90° triangle, where the lengths of the sides are in the ratio 1:√3:2, respectively.

Applications

Right triangles are used in various fields such as engineering, architecture, and physics, where the principles of trigonometry are applied to solve problems involving distances, angles, and heights.

See also

• Triangle
• Trigonometry
• Pythagorean theorem
• Special right triangles