Center of mass

Bird toy showing center of gravity

CoG stable

Center gravity 2

orbit3

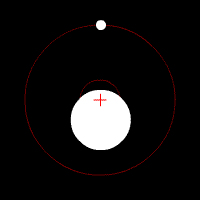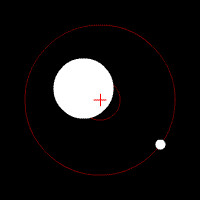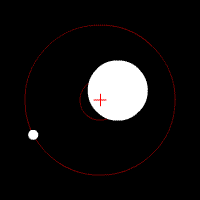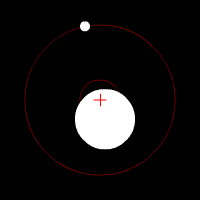
Center of mass is a fundamental concept in physics and engineering that represents the mean location of the distribution of mass in a body or system. It is a critical concept in the analysis of motion and is used to predict the behavior of objects in various physical situations, such as when they are subjected to forces or torques. The center of mass is a point where one can consider the entire mass of an object to be concentrated for the purpose of analysis.

Definition

The center of mass of an object or system of particles is the point at which the weighted relative position of the distributed mass sums to zero. Mathematically, it is defined as the average position of all the points in a body or system, weighted by their mass. For a system of particles, the center of mass is given by the formula:

\[ \mathbf{R}_{\text{cm}} = \frac{1}{M} \sum_{i} m_i \mathbf{r}_i \]

where \( \mathbf{R}_{\text{cm}} \) is the position vector of the center of mass, \( M \) is the total mass of the system, \( m_i \) is the mass of the \(i\)th particle, and \( \mathbf{r}_i \) is the position vector of the \(i\)th particle.

For a continuous distribution of mass, the center of mass is found using the integral form:

\[ \mathbf{R}_{\text{cm}} = \frac{1}{M} \int \mathbf{r} \, dm \]

where \( dm \) represents an infinitesimal element of mass at position \( \mathbf{r} \).

Properties

The center of mass has several important properties:

• It acts as the point where external forces can be applied to predict the motion of the object without causing rotation, assuming the body is free to move in space.
• In the absence of external forces, the center of mass of a system of particles moves in a straight line with constant velocity.
• The position of the center of mass is independent of the reference frame, meaning it is the same in all inertial frames.

Applications

The concept of the center of mass is widely used across various fields:

• In mechanics, it is used to analyze the motion of objects, including their translation and rotation around the center of mass.
• In astronomy, it helps in understanding the orbits of planets and stars, as they revolve around their common center of mass.
• In sports and human biomechanics, it is crucial for analyzing the balance and movements of athletes.
• In engineering, it is used in the design of structures, vehicles, and machinery to ensure stability and proper functioning.

Calculation

The calculation of the center of mass depends on the symmetry and density of the object. For simple geometric shapes with uniform density, the center of mass can often be determined from symmetry alone. For more complex shapes or density distributions, analytical or numerical methods may be required.

See Also

• Mass
• Physics
• Mechanics
• Torque
• Inertia
• Moment of inertia