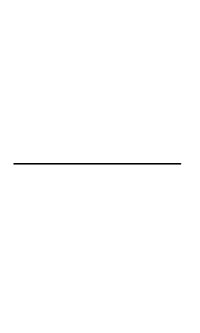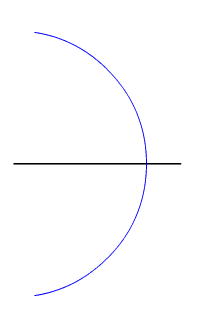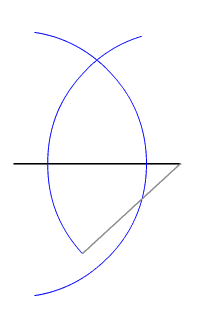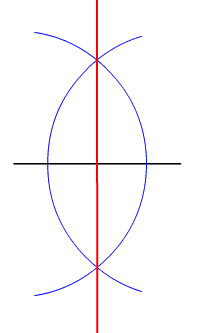Equidistant

Perpendicular bisector

Circumscribed Polygon

Equidistant refers to a concept in geometry and mathematics where a point or object is at an equal distance from two or more other points or objects. This principle is widely applied in various fields such as geography, physics, and engineering, demonstrating its fundamental importance across disciplines.

Definition

In geometry, an equidistant point is a location that is the same exact distance from two or more distinct points. A common example of this is the perpendicular bisector of a line segment, where every point on the bisector is equidistant from the segment's endpoints. Similarly, in the context of a circle, all points on the circumference are equidistant from the center of the circle.

Applications

Geography

In geography, the concept of equidistance is used in defining boundaries, especially in maritime territories. The equidistant principle may be applied to determine national boundaries where territories are equally distant from the coastlines of two different countries.

Physics

In physics, equidistant points are often involved in the study of wave interference, particularly in the context of constructive and destructive interference patterns. The points of constructive interference, where waves amplify each other, can be seen as equidistant from multiple wave sources under certain conditions.

Engineering

Engineering applications of equidistance include the design of objects and structures to have uniform stress distributions. For example, in the design of bridges or buildings, ensuring that certain points are equidistant from support structures can help in evenly distributing loads and stresses.

Mathematical Properties

The concept of equidistance is closely related to the properties of Euclidean geometry. It is often used in proofs and theorems, such as the perpendicular bisector theorem, which states that a point is on the perpendicular bisector of a segment if and only if it is equidistant from the segment's endpoints.

Equidistant Projections

In cartography, an equidistant projection is a map projection that preserves distances from a specific point or along a specific line. While no map projection can preserve true distances everywhere, equidistant projections are designed to maintain accurate distances from a central point or along certain lines, making them useful for specific navigational and geographical analyses.

Equidistant Resources
Need Help Finding a Doctor? Need help finding a doctor or specialist anywhere in the world? Explore our world directory. WikiMD's DocFinder can assist you in locating millions of physicians.	Medical Knowledge Access the latest research - Most recent articles Ongoing trials.

Translate to: East Asian 中文, 日本, 한국어, South Asian हिन्दी, Urdu, বাংলা, తెలుగు, தமிழ், ಕನ್ನಡ,
Southeast Asian Indonesian, Vietnamese, Thai, မြန်မာဘာသာ, European español, Deutsch, français, русский, português do Brasil, Italian, polski